|
This argument is the basis for Georg Cantor's theory that there are degrees of infinity, i.e. the infinity that represents the set of Natural numbers is not the same as the infinity that represents the set of Real numbers.
Consider the sets N = {0, 1, 2, �} of natural numbers and the set E = {0, 2, 4, �} of even numbers. Common sense would suggest that the set N is bigger than the set E because only half of the natural numbers are even. But if we were to list the members of each set then it can be seen that for every member of set N there is a corresponding member of set E.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | ... |
| ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ | ↓ |
| 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | ... |
It can be further proven that many other infinite sets share the same cardinality as the set of Natural numbers. Cantor denoted the infinity of elements in these sets with the cardinal number aleph-null 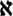 0 and larger infinite sets i.e. those without a one-to-one correspondence with the infinitude of Natural numbers are denoted 0 and larger infinite sets i.e. those without a one-to-one correspondence with the infinitude of Natural numbers are denoted 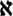 1, 1, 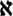 2, 2, 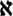 3 these are called transfinite numbers. 3 these are called transfinite numbers.
Now to Cantor's proof that there is not a one-to-one correspondence of the set of Real numbers with the infinitude of Natural numbers.
Consider a list of Real numbers between 0 and 1 where each number corresponds to a member of the set of Natural numbers i.e. a1 ⇒ 1, a2 ⇒ 2, a3 ⇒ 3, a4 ⇒ 4, an ⇒ n.
a1 = 0.890328754907861�
a2 = 0.528520654035861�
a3 = 0.247815759367324�
a4 = 0.082489564213887�
a5 = 0.420985387691245�
a6 = 0.143249526570604�
������������
an = 0.n1n2n3n4n5n6n7n8�nn�
We might then create a new number composed of the diagonal digits that are coloured red:
b = 0.827489� nn�
If we were to then add 1 to each digit in this number to create yet another new number e.g.
c = 0.938590�(nn+1)�
We would have created a number that could not possibly be in the original list as it would differ in at least one digit to any number in the original list.
The first digit must differ from the first digit of a1 so c ≠ a1. The second digit must differ from the second digit of a2 so c ≠ a2. The nth digit must differ from the nth digit of an so c ≠ an and so on for all the numbers in the list.
For further information see PlanetMath.org an excellent resource for all mathematical information and the following page which is specifically about Cantor's Diagonal Argument http://planetmath.org/encyclopedia/CantorsDiagonalArgument.html
| 
