|
Leonhard Euler (pronounced "oiler", not "yooler") was a Swiss mathematician and physicist. Leonhard Euler used the term "function" (first defined by Leibniz - 1694) to describe an expression involving various arguments; ie: y = F(x). Euler is credited with being one of the first to apply calculus to physics.
Born and educated in Switzerland, he worked as a professor of mathematics in St Petersburg, later in Berlin, and then returned to St Petersburg. He is considered to be the most prolific mathematician of all time. He dominated the eighteenth century mathematics and deduced many consequences of the then new calculus. He was completely blind for the last seventeen years of his life, during which time he produced almost half of his total output.
Euler was deeply religious throughout his life. The widely told anecdote that Euler challenged Denis Diderot at the court of Catherine the Great with "Sir, (a+bn)/n = x; hence God exists, reply!" is however, false.
Discoveries
He is the physicist who, with Daniel Bernoulli, established the law that the torque on a thin elastic beam is proportional to a measure of the elasticity of the material and the moment of inertia of a cross section, about an axis through the center of mass and perpendicular to the plane of the couple.
He also deduced a set of laws of motion in fluid dynamics from Newton's laws of motion that state:
| 1. | The force acting on a small element of a fluid is equal to the rate of change of its momentum. |
| 2. | The torque acting on a small element of a fluid is equal to the rate of change of its angular momentum.
|
In mathematics, he made important contributions to number theory as well as to the theory of differential equations. His contribution to analysis, for example, came through his synthesis of Leibniz's differential calculus with Newton's method of fluxions.
He established his fame early on by solving a long-standing problem:
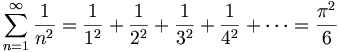
He also showed that for all real numbers x,
eix = cos(x) + i sin(x)
This is Euler's formula, which establishes the central role of the exponential function. In essence, all functions studied in elementary analysis are either variations of the exponential function or they are polynomials. The most remarkable formula in the world is an easy consequence.
In 1735, he defined the Euler-Mascheroni constant useful for differential equations:
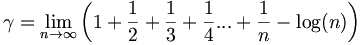
He is a co-discoverer of the Euler-Maclaurin formula which is an extremely useful tool for calculation of difficult integrals, sums and series.
Euler wrote Tentamen novae theoriae musicae in 1739 which was an attempt to combine mathematics and music; a biography comments that the work was "for musicians too advanced in its mathematics and for mathematicians too musical".
In economics, he showed that if each factor of production is paid the value of its marginal product, then (under constant returns to scale) the total income and output will be completely exhausted.
In geometry and algebraic topology, there is a relationship called Euler's Formula which relates the number of edges, vertices, and faces of a simply connected polyhedron. Given such a polyhedron, the sum of the vertices and the faces is always the number of edges plus two. i.e.: F - E + V = 2. The theorem also applies to any planar graph.
For nonplanar graphs, there is a generalization: If the graph can be embedded in a manifold M, then F - E + V = ?(M), where ? is the Euler characteristic of the manifold, a constant which is invariant under continuous deformations. The Euler characteristic of a simply-connected manifold such as a sphere or a plane is 2. A generalization of Euler's formula for arbitrary planar graphs exists: F - E + V - C = 1, where C is the number of components in the graph.
In 1736 Euler solved a problem known as the seven bridges of K�nigsberg, publishing a paper Solutio problematis ad geometriam situs pertinentis which may be the earliest application of graph theory or topology.
MacTutor biography of Euler:
http://www-history.mcs.st-andrews.ac.uk/history/Mathematicians/Euler.html
This article is licensed under the GNU Free Documentation License. It uses material from the Wikipedia article "Leonhard Euler".
| 
